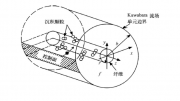
Kuwabara单纤维过滤模型用于分析纤维过滤介质表面尘粒捕集问题。如图 1所示, 圆柱纤维体垂直气流方向置于 Kuwabara流场单元的中心, 在控制面上随机释放的粒子受流体 Stokes拖拽力、重力及电场力等作用下被输送至纤维过滤介质表面附近, 因粒子与纤维表面间的范德华力而被捕集。此时, 被捕集的粒子作为新的捕集体对随后的来流粒子具有捕集作用。随着过滤过程的进行, 尘粒不断被捕集形成链状堆积结构, 即“粉尘树枝”结构, 引起纤维捕集效率的增加。在忽略外力场作用和粒子的布朗运动情形下,粒子仅受到流体的拖拽力, 因此将(1)式转化为图 1坐标系下空间对时间的变换规律后, 得到粒子运动轨迹方程为式中 τ为粒子运动的速度松弛时间, s;mp为粒子质量, kg;ux、uy为气流绕纤维的流动速度, m/s。该速度可由 Kuwabara流表示, 由文献 [ 6] 给出的 Ku-wabara流在极坐标下表示为式中 ur为径向速度, m/s;r为径向坐标, m;θ为极角坐标, rad;uθ为横向速度, m/s;c表示单纤维过滤模型的填充密度, c=(rf/b)2 ;rf为纤维半径, m;b为Kuwabara流场单元的半径, m;u0 为主流平均速度, m/ ,s(u0 =u∞ /(1 -c), u∞为未受干扰的来流速度,亦称过滤风速, 下同);Ku为 Kuwabara动力学因子,在图 1所示的直角坐标下, Kuwabara流速度可由以下关系获得dT2式中 St为表征粒子惯性的 Stokes数, 定义为 St= ρpu∞ d2pCm /18μrf;ρp为粒子密度, kg/m3 ;dp为粒子直径, m;μ为空气动力粘度, kg/m· s;Cm为粒子的肯宁汉滑移修正因子;其余各量定义见图 1。考虑到粒子在气流中随机分布特征, 将粒子运动的起始点随机置于图 1中的控制面上, 并进一步假设粒子的初始速度与粒子所在位置处流体速度相当考虑已捕集粒子对随后来流粒子捕集的影响时, 由已捕集粒子和纤维体构成的捕集体对粒子的捕集共同起作用, 捕集体形状因粒子的捕集而不断发生变化, 因此, 基于极限轨迹的单纤维捕集效率计算方法已不再适应。令 t时间内通过控制面的粒子数为 MG, 其中, 被捕集的粒子数为 MC, 并假设气流中粒子数浓度为 Cn, 个/m3 , 则如前所述, 本文讨论粒子直径 dp≥0.5 μm的情形, 并忽略其他外力场作用, 因此, 粒子捕集机制为拦截效应和惯性碰撞。在数值求解粒子运动轨迹时, 粒子运动时间步长为 Δt=0.01 ～ 0.05, 其中小粒子取下限, 大粒子取上限。计算所需基本参数按如下条件规定:空气动力粘度取 1.8192 ×10-5 kg/(m· s);单纤维过滤模型的填充密度分别为 0.01、0.03和 0.05;粒子直径取为 0.5、1和 1.5 μm, 纤维直径为 10 μm;纤维长度为 50 μm。由于气流中粒子分布的随机特征, 每次模拟结果为一次随机事件, 因此, 在相同计算条件下执行多次模拟结果的平均才具有统计意义, 在本文的计算中, 每种计算条件下执图 2显示的是典型的单纤维过滤介质表面的粒子捕集过程。从图 2中可以看出, 粒子在过滤介质表面的捕集过程可分为 3 个典型的阶段, 分别为初始捕集阶段、纤维-树枝捕集阶段和完全树枝捕集阶段。当过滤介质处于清洁状态时, 粒子被过滤介质直接捕集, 捕集效率增加缓慢, 这一阶段称之为初始捕集阶段或稳态过滤阶段。随着过滤介质上捕集的粒子数增多, 开始有粉尘树枝生成, 此时一部分粒子被过滤介质捕集, 而另一部分粒子则被已捕集的粒子捕集, 捕集效率迅速增加, 这一阶段称之为纤维-树枝捕集阶段。随着粉尘树枝进一步长大, 绝大部分粒子被粉尘树枝捕集, 系统进入“尘滤尘”阶段,也即完全树枝捕集阶段。粒子在单纤维过滤介质表面捕集呈现的 3个阶段对应于实际过滤中 3个典型的过滤阶段, 即稳态过滤阶段、过渡过滤阶段和滤饼图 3给出的是不同 St数下的粉尘树枝结构。模拟计算所取参数如下:粒子直径 dp =1 μm, 单纤维过滤模型填充密度 c=0.03, St数分别取为 2.47、 0.62和 0.06。通过改变粒子的密度和过滤风速取得相应的 St数值, 捕集的最大粒子数规定为800个。图 3给出的是不同 St数下的粉尘树枝结构。模拟计算所取参数如下:粒子直径 dp =1 μm, 单纤维过滤模型填充密度 c=0.03, St数分别取为 2.47、 0.62和 0.06。通过改变粒子的密度和过滤风速取得相应的 St数值, 捕集的最大粒子数规定为800个。从图 3中可以看出, St数对粉尘树枝的形态影响明显。当 St数较大时, 粒子捕集形成的粉尘树枝结构不明显, 只在沉积物上层出现细小的粉尘树枝。粒子在沿 Z轴方向的分布也较为均匀, 这一结果与文献[ 8]的实验观察结果一致(见图 4(a));当 St数较小时, 粒子捕集形成的粉尘树枝结构明显, 沿 Z轴方向的分布极不均匀, 甚至在局部地方出现较大的粉尘絮团, 这一结果也同样得到了实验的证实粉尘树枝的形态及粒子的分布依赖于 St数的原因是:在小 St数下, 纤维捕捉到粒子的概率小, 一旦有粒子在纤维上捕集, 则该点捕捉到粒子的概率数下, 粒子在纤维体附近的运动轨迹较弯曲, 形成的遮挡区域较大[ 10] , 从而在纤维表面形成分叉显著的粉尘树枝结构;相反, 在大 St数下, 纤维过滤介质上各点捕捉到粒子的概率较大, 粉尘树枝的优势生长减弱, 粒子在纤维体附近的运动轨迹也较平直, 形成的遮挡区域也就较小, 从而粒子捕集形成的粉尘树枝结构不明显。另外, 从图 3中还可以看出, St数由 2.47变化到 0.62, 沉积物由紧密的堆积结构变化到分叉显著的粉尘树枝结构, 粒子的分布逐渐向纤维前驻点附近聚集。但 St数由 0.62变化到 0.06, 粒子分布又逐渐向纤维前驻点两侧分散。从中可看出, 粒子在纤维过滤介质表面的分布角度随 St数增大经历两个阶段性变化:起初, 粒子分布角度随 St数减小而减小;随后, 随 St数减小而增大。本模拟中, 粒子在过滤介质表面的最小分布角度出现在 St=0.62。图 5显示的是单纤维过滤模型的填充密度分别为 0.01、0.03和 0.05时的粉尘树枝形态。模拟计算所需参数规定为:粒子直径为 1 μm, 粒子密度为1 g/cm3 , 过滤风速为 0.2 m/s。从图 5中可以看出,填充密度为 0.01时, 粒子捕集形成的粉尘树枝数目较少, 但单个树枝结构尺度大;填充密度为 0.03和0.05两种情形下的粉尘树枝结构较为相似, 且粉尘树枝沿 Z轴方向分布都较为均匀。图 6所示的是 St数对捕集粒子数和单纤维捕集效率的影响。模拟计算中所需参数规定如下:粒子直径取 1 μm, 单纤维过滤模型填充密度为 c= 0.03, St数分别为 0.12、1.5和 2.5, 最大捕集粒子数设为 800个。图 6(a)给出的是不同 St数下捕集粒子数与释放粒子数的关系曲线。其中横坐标表示的是控制面上释放的粒子数, 纵坐标表示的是捕集的粒子数。由式(13)可知, 释放粒子数与过滤时间成比例, 因此, 图 6(a)中横坐标实质反映的是过滤时间。从图 6(a)中可以看出, 捕集粒子数先随释放粒子数增加而呈缓慢增加, 且 St数越小, 缓慢增加的过程越长;随着释放粒子数的进一步增加, 捕集粒子数出现一个快速增加过程;此后, 捕集粒子数随释放粒子数呈近似线性增加关系, 且这种线性增加率在 3种 St数情形下也较为接近, 这说明 St数对粒子的捕集影响已大为减弱, 而粉尘树枝对粒子的捕集图 6(b)给出的是不同 St数下捕集粒子数对单纤维捕集效率的影响。横坐标表示捕集粒子数, 纵坐标表示无量纲捕集效率(单纤维捕集效率与清洁纤维捕集效率之比)。不同 St数下清洁纤维捕集效率也表示在图中, 从图 6(b)可以看出, 在粒子捕集的初始阶段, St数对粒子的捕集起决定作用, St数越大, 单纤维捕集效率越高, 这与经典纤维过滤理论的分析结果一致[ 11] 。随着捕集粒子数的增多, 3种情形下, 单纤维捕集效率均呈线性增加, 但增加的幅度有所不同, St数越大, 单纤维捕集效率的增加幅度越小。在捕集粒子数为 800 个时, 3 种情形的单纤维捕集效率均达到 3.5%左右, 这进一步说明在粒子捕集的后期阶段, 粉尘树枝对粒子捕集起主导作用。