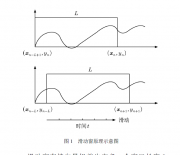
混沌时间序列是由非线性确定性系统产生的一种介于确定性与随机性之间的非线性动力学现象. 它是有序与无序、确定性与随机性的中间态,宏观上表现为无序无律的混乱运动以及对初值十分敏感的 “蝴蝶效应”, 微观上呈现无穷嵌套的几何自相似性. 不同于随机时间序列, 混沌时间序列具有短期的可预测性和长期的不可预测性 [1,2]. 混沌系统在现实生活中普遍存在, 近年来随着人们对混沌理论研究的不断深入, 它在许多实际系统中得以广泛应用, 如生物医学、声学、化学、通讯、交通、气候天气、电力负荷、财经金融等. 因此, 混沌时间序列的建模和预测已成为混沌信号处理领域中一个非常重要的研究方向. 按照建模原理的不同,已有混沌时间序列的预测方法有多项式法 [3]、模糊理论法[4,5]、信息熵法[6]、回声状态网络法[7,8]、支持向量机[9,10] 等. 其中基于结构风险最小化原则的支持向量机 (support vector machine, SVM)[11,12]因其在小样本的情况下具有较好的泛化能力而备受关注. 用支持向量机来进行混沌时间序列的建模和预测是一种有效的手段, 其中的一个典型代表就是滑动窗 (sliding window, SW) 支持向量机 [13−15],其原理如图1 所示.滑动窗支持向量机首先定义一个窗口长度 L,每次都是基于窗口内的数据 {(xi,yi)}i=n−L+1 来进行支持向量机的建模, 而窗口外面的数据则完全被抛弃. 这其实是一种遗忘机制, 也就是说窗口外面的数据被完全遗忘掉. 而当有新的数据 (xn+1,yn+1)要进来时, 将离当前时刻最远的数据 (xn−L,yn−L)挤出窗口, 然后基于新窗口内的数据 {(xi,yi)}in=+n1−L对模型进行调整. 这种窗口更新机制的思想是离当前时刻最远的数据对下一个数据预测的影响比较小. 这种以时间作为衡量标准的窗口更新机制是有局限性, 如用离线学习方法进行混沌时间序列建模时, 在对当前时刻数据进行预测时, 前一刻的数据并没有用来建模, 而同样可以取得比较好的预测效果. 这就说明离当前时刻比较远的数据对混沌时间序列模型的建立是有贡献的, 并且这种贡献并不一定比离当前时刻比较近的数据差.抛弃. 这其实是一种遗忘机制, 也就是说窗口外面的数据被完全遗忘掉. 而当有新的数据 (xn+1,yn+1)要进来时, 将离当前时刻最远的数据 (xn−L,yn−L)挤出窗口, 然后基于新窗口内的数据 {(xi,yi)}in=+n1−L对模型进行调整. 这种窗口更新机制的思想是离当前时刻最远的数据对下一个数据预测的影响比较小. 这种以时间作为衡量标准的窗口更新机制是有局限性, 如用离线学习方法进行混沌时间序列建模时, 在对当前时刻数据进行预测时, 前一刻的数据并没有用来建模, 而同样可以取得比较好的预测效果. 这就说明离当前时刻比较远的数据对混沌时间序列模型的建立是有贡献的, 并且这种贡献并不一定比离当前时刻比较近的数据差.因此, 本文结合最小二乘支持向量回归机(least squares support vector regression, LSSVR)[16,17] 提出一种新的窗口更新机制, 即过滤窗(filtering window, FW), 这种窗口更新机制 “过滤” 数据时并不是以时间作为衡量准则, 而是以对混沌时间序列模型的贡献大小来作为衡量准则. 在这种机制里, 可以把窗口看成是一张 “网”, 一个个数据可以看成是一个个 “粒子”, “粒度” 的大小取决于数据对混沌时间序列模型的贡献程度, 贡献越大, “粒度” 也就越大,反之则越小. 不过这张 “网” 的网空是自适应变化的, 目的是保持“网” 中“粒子” 的数目不变化. 刚落入 “网” 中的 “粒子” 是否能留在 “网” 中, 以及 “网” 中哪一个 “粒子” 将被漏掉, 完全取决于这些 “粒子” “粒度” 的大小. 这样以来, 在具有相同窗口尺度 L 的情况下, 与滑动窗最小二乘支持向量回归机(SW-LSSVR) 比较, 过滤窗最小二乘支持向量回归机 (FW-LSSVR) 所建立的混沌时间序列模型具有更好的预测精度, 这也同时意味着在相同混沌时间序列模型预测精度的情况下, FW-LSSVR 需要的窗口长度 L 比较小, 其实时性自然较好. 另外, 即使在相同的窗口尺度下, FW-LSSVR 的模型更新速度也比SW-LSSVR 快, 即实时性也比较好. 最后, 用一些典型的混沌时间序列例子来验证本文所提算法在混沌时间序列建模和预测中的有效性和可行性.无论对算法 SW-LSSVR, 还是对 FW-LSSVR, RMSE 都随着窗口长度 L 的增加而逐渐减小, 最后趋于稳定而几乎接近相等, 也就是说混沌时间序列预测的精度随着窗口长度 L 的增加而逐渐提高, 最后这两种算法的预测精度几乎相等. 可是, 相比较而言, FW-LSSVR 预测产生的 RMSE 随窗口长度 L的增加要减少得更快. 换句话说, FW-LSSVR 以更快的速度接近稳定. 这就会产生要达到相同的预测精度, FW-LSSVR 需要较短的窗口长度 L, 也就意味着需要较少的 “粒子”, 而较少的 “粒子” 往往寓意着较短的时间, 较好的实时性. 同时, 这也说明了过滤窗口 “过滤粒子” 的有效性. 图 3 给出了在预测完 1000 个样本后, 过滤窗中 “粒子” 的状态.从图3 可以看出, 对于混沌时间序列Kawakami来说, 过滤窗中的 “粒子” 大部分集中在前半部分;对于 Heron 来说, 过滤窗中的 “粒子” 分布比较均匀 (其他混沌时间序列不是像 Kawakami 就是像Heron, 没有过滤窗中大部分 “粒子” 都集中在后面的情况, 在此予以省略). 无论是哪一种, 过滤窗中的 “粒子” 随着时间的推移更新频率都比较低, 这就是 FW-LSSVR 的计算代价比 SW-LSSVR 低的一个重要原因. 由图 3 可知, 过滤窗中大部分 “粒子” 都分布在极值点, 也就是靠近图形的两边, 这与支持向量机中支持向量的分布类似 [7], 也就是说 FS-LSSVR 把比较重要的 “粒子” 留在了窗口当中, 证明了过滤窗口过滤 “粒子” 的有效性. 另外, 从图 3中还可以看出, 位于图形中部过滤窗口中的 “粒子” 大部分集中在前面, 这主要是因为后面位于中间部分的粒子由于和前面中间部分的 “粒子” 相似而不能进入到过滤窗中, 这就减轻了过滤窗的更新频率,从表 1 可以看出, 对同一个混沌时间序列, 当预测精度即RMSE 趋于稳定时, FW-LSSVR 需要较短的窗口长度, 也就预示着 FW-LSSVR 需要较短的预测时间, 这一点可以从表 1 中每一个混沌时间序列实验的第一行和第三行看出来. 在预测精度几乎相同的情况下, 其预测误差情况如图 4 所示.从图 4 可以看出, 在预测精度几乎相等的情况下, FW-LSSVR 需要较少的 “粒子”. 另外, 还可以从图4 中看出, 在开始阶段预测误差较大, 而随着时间序列的推移, 精度趋于稳定. 这主要是因为, 在开始阶段, 算法刚刚启动, 窗口的长度不够, 算法没有足够滑动窗在滑动的过程中, 只是简单地将最远的数据给抛弃掉, 将最近的数据移入窗口. 而在建模的过程中, 最远的数据对模型的贡献程度并不一定比最近的差. 滑动窗这种将最远的数据给抛弃掉的做法存在不妥之处. 然而, 过滤窗口则不同, 它就像是张 “网”, 每一个数据就是一个 “粒子”, 同时给每一个 “粒子” 定义一个 “粒度”, 根据 “粒度” 的大小决定哪些 “粒子” 将留在 “网” 中, 哪个 “粒子” 将被的学习能力而导致预测误差较大, 而随着窗口长度的增长, 预测误差逐渐减小. 当窗口长度增长到某一个值时, 预测精度趋于稳定, 就不需要增长窗口长度了, 若继续增长, 只会增添算法的计算量, 影响其实时性. 在和 FW-LSSVR 窗口长度相等的情况下, SW-LSSVR 的预测误差如图 5 所示. 从图 5 可以看出, 在窗口长度相同的情况, SW-LSSVR 的预测误差较大, 这一点也可以从表 1 中得到印证. 同时, 这也说明了滑动窗口策略存在的缺陷, 而过滤窗口是有效的.遗漏. 新来的 “粒子” 能否留在 “网” 中就看其 “粒度” 的大小, 而不是看时间的远近. 而 “粒度” 就是根据 “粒子” 对模型的贡献程度来定义的, 这样选择出来的“粒子” 自然对模型的贡献程度比较大, 过滤窗口这种淘汰机制自然也要比滑动窗口简单的遗忘机制要好. 因而, 与滑动窗最小二乘支持向量回归机相比较, 过滤窗最小二乘支持向量机具有较好的实时性和较高的精度.