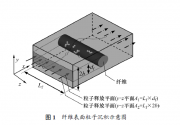
工业生产、汽车尾气及自然作用产生的大量微粒影响着大气环境[1]，尤其是气溶胶粒子(指悬浮于空气中的固体或液体颗粒物)，粒径主要分布在 10−3~102 μm，对人类生存环境和健康产生了严重的影响。纤维过滤是控制微粒排放并完全达到国家环保标准的有效手段之一。实践研究表明[2−4]：纤维表面粒子沉积形成链状堆积结构，即所谓的“粉尘树枝”，是引起过滤特性(过滤效率和压降)变化，并最终导致过滤设备失效的根本原因。忽略粒子碰撞反弹作用，在惯性碰撞、扩散及静电作用下，纤维表面粒子沉积行为已有许多研究，如 Payatakes 等[5−6]基于理想粉尘树枝结构模型假设，建立了一系列描述粉尘树枝生长动力学数学模型；Kanaoka 等[7−9]利用随机模拟方法研究了惯性碰撞、扩散及静电联合作用下纤维表面粉尘树枝生长行为；Li 等[10−11]考虑了粒子间黏附力作用，利用 DEM模拟方法研究了惯性碰撞和静电作用下纤维表面粒子沉积行为。考虑粒子碰撞反弹作用纤维表面粒子沉积行为的研究也有少量报道，如 Tsiang 等[12]忽略了粒子碰撞反弹后的运动特性，采用随机模拟方法研究了纤维表面粒子沉积与反弹行为，并与实验结果进行了比较；Athanasies 等[13]忽略粒子间相互作用，研究了粒子与纤维表面的碰撞反弹行为，并与实验结果作了比较。Kasper 等[14−15]实验研究了粒子碰撞反弹作用下纤维表面沉积物形态结构特征及纤维捕集效率变化，但仍缺乏该过程微观角度的细节信息。本文将随机模拟方法和粒子碰撞反弹理论相结合，并考虑粒子碰撞反弹后的运动特性，对纤维表面粒子沉积和反弹行为进行直接数值模拟，分析粒子碰撞反弹行为对沉积物形态结构和纤维捕集效率影响，以便为工程应用提供理论参考。图 1 所示为纤维表面粒子沉积示意图。由图 1 可知：圆柱状纤维垂直于主流方向置于流场，在粒子释放平面上(远离纤维的上游)随机释放一粒子，该粒子受 Stokes 力、重力、随机力及电场力等作用被输送至纤维表面附近而被捕集，而捕集的粒子则作为新的捕集体对随后输送来的粒子具有捕集作用。随着过滤过程的进行，尘粒不断被捕集，形成链状的堆积结构，即“粉尘树枝”结构，这样便引起纤维过滤特性的变化。为简便起见，先对粒子相作如下假设：(1) 粒子 相为稀相，即不考虑输送过程中粒子之间的相互碰撞，仅考虑单个粒子的运动特性，并且气流与粒子间的作用为单向耦合作用，粒子的存在不影响流场；(2) 进入计算区域的粒子均为规则球体，具有相同的密度p；(3) 当单个粒子在流场中运动时，只考虑气相场的Stokes 阻力，忽略随机力和外力场作用；(4) 忽略沉积粒子对流场变化的影响。在上述假定下, 根据牛顿第二定律，单个粒子运动的矢量方程表示为其中：u 为表观速度，uu(/ 1)c，m/s； c为过滤单元容密度，定义为纤维体积与 Kuwabara 过滤单元体积比(亦称填充密度)；r 为径向坐标，m；为极坐标，rad；b 为 Kuwabara 流场单元半径(见图 2)，m；Kn 为 Knudsen 数；l 为空气分子平均自由程，m。 对给定的初始速度和位置，采用四阶 Rung-Kutta方法对式(2)和(3)数值积分获得粒子的运动轨迹。 1.2  粒子碰撞反弹模型 已有许多研究者对物体表面粒子碰撞反弹机理进行研究[18−23]，本文采用 Dahneke[21−23]碰撞反弹理论分析纤维过滤中粒子碰撞反弹行为。如图 3 所示：输送粒子以速度 vi与纤维或已沉积粒子发生碰撞，设沿碰撞表面的法向碰撞速度分量为 vi,n，切向碰撞速度分量为 vi,t；粒子反弹速度为 vr，沿碰撞表面的法向反弹速度分量为 vr,n，切向反弹速度分量为 vr,t。 式中：Ek, in 为粒子沿法向方向的碰撞动能； Ek, rn 为粒子沿法向方向的反弹动能；Ep, i 和 Ep, r 分别为粒子碰撞前后的动力学势能；e 为碰撞弹性恢复系数。由式(7)可知：粒子被捕集的条件为反弹动能 Ek, in=0，假设  Ep, i =Ep, r =Ew，则粒子反弹临界速度 vcr 表示为： 根据上述粒子碰撞反弹模型可知：粒子碰撞反弹作用不仅与过滤参数有关，还与粒子和纤维的材料参数有关。为获得明确的计算结果，选取不同 H(Hamake常数)作为影响粒子碰撞反弹作用的综合参量，对几种典型过滤工况下纤维表面粒子沉积和反弹行为进行数反弹的频率也较高，如粒径为 5 μm 的粒子几乎全部与纤维碰撞并发生反弹作用；而较小粒径粒子与纤维碰撞的频率较低，例如，粒径为0.5 μm 的粒子因惯性小几乎全部未与纤维碰撞；粒子为 1 μm 的粒子与纤维发生碰撞频率较高，但因反弹临界速度较大，碰撞不同H下输送粒子与沉积粒子碰撞反弹后的运动轨迹如图5 所示。由图5 可知：随着H 减小，粒子发生碰撞反弹频率增加。同时，也观察到输送粒子与沉积物外侧粒子碰撞反弹后，容易逃离过滤单元；而与沉积物内部粒子碰撞后，经过多次碰撞反弹作用，最终因能量损耗而被捕集。这表明粒子与沉积物发生碰撞反弹作用后仍有可能被捕集。下纤维表面沉积物的形态结构特征文献[7, 25]已经讨论过。即随着 St 数增大，沉积物形态结构由分叉显著的树枝状结构向紧密结构演变；当拦截参数 Nr (Nr=dp/df) 和粒径分散度增大时，沉积物形态结构表现出更加开放、疏松的结构。为考察粒子碰撞反弹作用对沉积物形态结构影响，选取 4 种典型过滤工况，取不同 H 进行数值计算，结果见图 6。图 6 中，深色粒子表示纤维捕集粒子，浅色粒子表示被沉积粒子捕图 6(a)所示为 Nr=0.07，St=0.66 情形下不同 H 纤维表面沉积物形态结构。具体计算参数取值为：df30 μm，dp2 μm，u0.8 m/s， 1 g/cm3，c0.05。从图 6(a)可以看出：随着H 变小，沉积物由树枝状结构向紧密结构演变，但未观察到粒子反弹作用对沉积物分布角度 θ 有明显变化。 将粒子密度增至 2 g/cm3，相应St=1.32，其余参数同图 6(a)。此条件下不同H 下纤维表面沉积物形态结构如图 6(b)所示。由于粒子惯性作用增大，沉积物的高度明显低于图 6(a)中的高度；粒子反弹作用仍对沉积物形态结构产生影响，但不如图 6(a)所示的影响显著。图 6(c)所示为Nr =1，St =9.88 情形下，不同H 下纤维表面沉积物形态结构。具体计算参数取值为：df 2 μm，dp2 μm，u 0.8 m/s， 1 g/cm3，c0.01。由图 6(c)可知：随着H 变小，沉积物中粉尘树枝的高度及分散程度均有所降低，但不如图 6(a)所示的影响显著。此外，随着H 变小，沉积物中由纤维捕集的粒子数略有增加，这是由于粒子之间的反弹作用降低了沉积物捕集粒子的能力，从而减缓了粉尘树枝的生长，增加了纤维捕集粒子的概率。图 6(d)所示为多分散粒子过滤情形下粒子反弹作用对沉积物形态结构的影响。本文考虑粒子粒径服从正态分布情形，粒径累积分布函数为：在此基础上，进一步讨论几种典型过滤条件下，粒子碰撞反弹作用对荷尘状态过滤单元捕集效率的影响。图8 所示为 Nr0.07，St0.66 情形下，不同H 下过滤单元捕集效率 ηe 随无量纲沉积量 Vc 的变化关系曲线。Vc 定义为沉积粒子体积比纤维体积。由于此过滤条件粒子直径远小于纤维直径，故该条件属于较低拦截参数过滤情形，具体计算参数取值与图 6(a)中的相同。由图 8 可看出：若忽略粒子碰撞反弹作用，则ηe 随 Vc 呈近似线性增加。粒子碰撞反弹作用对纤维捕集效率的降低作用十分明显，且 Vc 越大影响越显著。在这种情况下，ηe 随Vc 的变化关系出现了2 个阶段性变化特征，但各阶段变化关系仍满足近似线性，且第一阶段(即过滤初期) ηe 增速要快于第二阶段。文献[14]的实验研究中也观察到类似现象。这是由于在过滤初期，粒子主要沉积于纤维前驻点附近区域，受驻点附近气流的影响，粒子的碰撞反弹作用较弱，故对纤维捕集效率的影响较小。随着沉积的粒子数增加，沉积物生长至主流区，形成第二阶段(即过滤稳定期)。由于过滤风速增加，粒子碰撞速度增大，碰撞反弹作用也随之增强，对捕集效率的降低作用开始显现，但因粉尘树枝对捕集效率的贡献作用在增大。因此，ηe 随Vc变化仍表现出增加的趋势。过滤的起始阶段(曲线起点，亦即清洁状态纤维过滤阶段)，所有 H 下捕集效率几乎相等，这表明此过滤条件下粒子与纤维碰撞后未发生反弹作用。图9 所示为 Nr=0.07，St=1.32 不同H 下过滤单元捕集效率 随无量纲沉积量 Vc 的变化关系曲线，具体参数取值同图 6(b)。由图 9 可知：由于粒子的惯性作用增强，忽略粒子的碰撞反弹作用过滤单元捕集效率增加明显， 2 g/cm3 时清洁状态下过滤单元捕集效率接近 1 g/cm3 时的 50 倍；当考虑粒子碰撞反弹作用后，由于粒子的密度增加，根据式(8)，碰撞反弹临界速度将降低，反弹作用明显增强；当 H1×10−19 J时，清洁状态下过滤单元捕集效率下降至 1%以下，与 1 g/cm3 时相当，且当 Vc 大于 0.02 时，ηe 随 Vc增加几乎保持不变。图 10 所示为Nr1，St9.87 情形下，不同H 下过滤单元捕集效率 ηe 随无量纲沉积量 Vc 的变化关系曲线。由于此过滤条件粒子直径与纤维直径相当，故该条件属于较高拦截参数过滤情形，具体计算参数取值与图 6(c)的相同。由图 10 可知：所有 H 下，ηe 随 Vc的变化均呈现近似线性增加关系，未表现出 2 个阶段性变化特征，这是由于此计算条件下粒子和纤维的特征几何尺度相当，极少量的沉积粒子数即可占据纤维的前驻点区域(见图 6(c))；此外，由于粒子具有较大惯性，故受驻点附近气流流动的影响很弱。因此，第一阶段的沉积特征不明显，整个粒子的沉积过程主要是第二阶段。